9. Vases
In front of you are two irregular, unrated vases: the first can hold 3 liters and the second 5. Explain how you can use it to get exactly one liter of liquid.
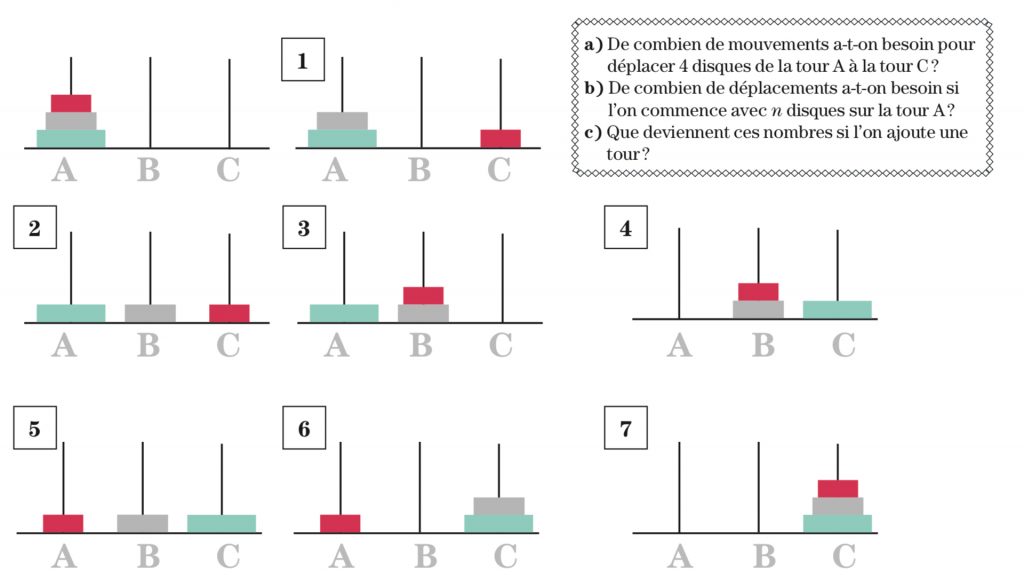
10. Hanoi Towers
This is a nice toy that consists of three rods and discs of different sizes. To win, you only need to move the discs from tower A to tower C. But be careful: you can only move one disc at a time and you can never drop the disc onto a smaller disk. Here, for example, like moving three discs.
11. Soaked touch
the game Warship It consists in finding enemy positions on a chessboard of 10 squares by 10 squares by trying a new square at each turn. For being so unlucky, you’ll need 100 spins to win. Let us replace this network with an infinite network with a square center (0,0). All other cells are identified by their coordinates (row and column) with positive and negative integers. Assume you are searching for one enemy ship. Being unlucky you will need unlimited time to find it.
Develop a search technology that ensures you can find the enemy ship without the need for endless experiments.
12. The paradox of birthdays
To simplify the problem, we’ll assume that a year always has 365 days in it.
It happens that in the group there are at least two people who have the same birthday. In a group of 366 people, at least two are sure to share their birthdate. In a group of 400, this is almost certain to happen. However, in a group of two, there is only a slight chance their birthdays are the same (1 chance in 365 in fact). Complete the sentence using the smallest number that makes it correct.
In a group of ____ people, there is a more than 50% chance that two of them will be on the same date of birth.
13. Le nombre d’or
Curiously, the golden number φ ≈ 1.618 has the same decimal development as 1 / φ ≈ 0.618 (i.e. the same sequence of numbers after the decimal point).
a) Next to 1 and -1, find another number with the same property.
B) Find an infinite number of numbers that have this property and show those numbers
That I found is different.
14. What a strange shape!
To create it, we start with a black circle of 1 square meter. Then we place in each circle a smaller circle between the edge and center of the previous circle, alternating between white and black. The process is repeated an infinite number of times. The first steps are reproduced in the opposite direction, but the final shape will have an infinite level of detail that cannot be drawn.
What is the area of ​​the shaded part?
We want to get to 555-1849, but we require 555-1749. An uneasy discussion ensues … To avoid this, imagine a new law that requires all phone numbers to contain at least two different numbers. Thus, by designating 555-1849, it becomes impossible to give the model numbers X55-1849, 55X-1849, 555-X849, 555-1X49, 555-18X9 and 555-184X.
a) Simon says he made calculations and that under this new law, we will have to assign numbers 64 times fewer (numbers are 7 numbers). Track his thinking and explain why he was wrong.
B) Show Simon how to obey the law by assigning numbers only ten times less.
At the fairground booth, 10 young men are queued and look straight ahead. Within an hour, a blue or red hat would be placed on their heads. Nobody will see the color of their own hat or the hats of the participants behind them. But everyone will see all the hats up front very well. Starting with the last person on the line, they will be asked to guess the color of their hat. Little kids who guess the color correctly will win $ 100. Before the start of the game, the participants are allowed to talk to each other freely, but once the hats are in place, they can only take turns speaking and they will have to limit themselves to guessing the color of their hat. What is the strategy that always allows at least 9 guys to win the jackpot?
“Subtly charming problem solver. Extreme tv enthusiast. Web scholar. Evil beer expert. Music nerd. Food junkie.”